Tipo de dimensionamento com seqüências de Lucas
A relação entre o texto e o resto de uma página é uma das principais características de qualquer design.
Ritmo, ênfase e tom são comprometidos sem o tipo corretamente dimensionado. No entanto, a seleção de tamanhos de texto geralmente é uma experiência dolorosa e frustrante, sem ponto de partida padronizado para nos informar.
Como resultado, freqüentemente encontramos designers de web recorrendo às opções padrão apresentadas pelos aplicativos - 8pt, 10pt, 12pt, 14pt, 18pt - por falta de uma solução melhor.
Essa melhor solução é definir tamanhos de tipos não por capricho individual, mas de acordo com um sistema predeterminado; um sistema simples de usar, prático de implementar na Web e, o mais importante, flexível o suficiente para permitir aos projetistas uma gama completa de expressões. Sugestão: a sequência de Lucas.
Sequências Lucas
A seqüência de Fibonacci - registrada primeiramente no oeste durante o 13o século por Leonardo Fibonacci - é o seguinte conjunto de inteiros (números inteiros):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987… ad infinitum
A sequência recebeu o nome de Fibonacci, do eminente matemático francês do século XIX, François Édouard Lucas, que produziu uma sequência semelhante, a que ele se referiu como Lucas Numbers:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843… ad infinitum
A seqüência de Fibonacci e os números de Lucas são variações específicas da seqüência genérica de Lucas.
Seqüências de Lucas e seqüências inteiras em geral têm sido objeto de uma vida inteira de estudo para numerosos matemáticos realizados, então vamos resumir o conceito da seguinte forma:
- Qualquer número dado na seqüência é a soma dos dois números anteriores, conforme descrito nesta fórmula: n = n-1 + n-2
- Os dois primeiros números da sequência - conhecidos como números iniciais - são selecionados arbitrariamente.
Por que usar uma seqüência de Lucas para definir o tipo?
As Sequências de Lucas, particularmente na forma da Sequência de Fibonacci, têm uma estreita relação com a Proporção Áurea, que é repetida ao longo da natureza em conchas, teias de aranha, formações de nuvens e inúmeras outras maravilhas naturais. Há fortes evidências que sugerem que qualquer coisa que achemos visualmente atraente é devido à relação dessa forma com a proporção áurea.
Mais importante, Lucas Sequences nos fornece uma estrutura escalável para definir o tipo que é ao mesmo tempo gracioso e rítmico.
Determinando nosso primeiro número de sementes
Há muito debate sobre o tamanho correto do texto do corpo para um site. 12px ainda é o mais comum, mas não é incomum ver algo de 10px a 16px. Isso nasce substancialmente da falta de compreensão do que as medições de fonte realmente significam. Estranhamente, para aqueles de nós acostumados à padronização - ou pelo menos às aspirações de padronização - não existe uma medida padrão no design de tipos; dois designers de tipos diferentes, desenhando exatamente o mesmo design em software de produção de fontes, provavelmente desenharão em tamanhos diferentes. A variação entre diferentes tipos de letra é, sem surpresa, muito comum.

A resposta para onde começar é irritantemente simples; nosso tamanho de texto padrão será 1em, o que significa que nosso primeiro número de semente será 1.
Há uma série de benefícios para usar o 1em como nosso ponto de partida: como uma unidade relativa de medição, um em é bem adequado para o design responsivo; usando ems e múltiplos de ems, podemos redimensionar todo o nosso esquema alterando o tamanho básico da fonte; finalmente, é um ajuste conceitual puro com a nossa sequência de Lucas e servirá para nos lembrar da seqüência de números precisos se precisarmos revisitar o design mais tarde.
Não há nada de errado em usar porcentagens em vez de ems, ou mesmo pixels ou pontos, mas o em é mais do que provável o futuro do web design, então podemos nos acostumar com isso.
Determinando nosso segundo número de sementes
Existem inúmeras estratégias abertas para determinar nosso segundo número de sementes. Alguns designers têm uma preferência específica e escolheriam 1.2em ou algo parecido. Outros designers, que gostam do misticismo da Proporção Áurea, gostariam de usar o 1.618em.
Uma solução mais prática é determinar o segundo número de sementes usando a altura da linha do texto do corpo. No entanto, como a altura da linha geralmente é ditada pelo comprimento da linha e o comprimento da linha é determinado por uma grade, ela é mais adequada para impressão ou design de web não responsivo. Porque estamos olhando para o futuro e o futuro é responsivo, não funcionará para nós.
O que nos resta, em parte por um processo de eliminação e em parte devido à sua adequação, é a altura x do tipo. Ou, mais especificamente, a relação entre a altura x e o resto do glifo.
Uma característica do bom design é a repetição de elementos-chave, e carregar as proporções do tipo até a página como um todo é uma grande oportunidade para reconhecer o trabalho do designer de tipos e imbuir nosso design com um pouco do caráter do tipo.
Encontrando nossa altura x
Para encontrar a altura x de sua fonte, precisamos abrir algo como o Photoshop ou o Illustrator e adicionar um texto que inclua um ascendente (por exemplo, 'd') e a letra 'x'. Se você estiver usando um editor de bitmap como o Photoshop, defina o texto o maior possível para garantir um resultado preciso. Nestes exemplos eu configurei a fonte para 500pt para medi-la.
Em seguida, meça a altura da linha ascendente até a linha de base e a altura da parte superior do x à linha de base.
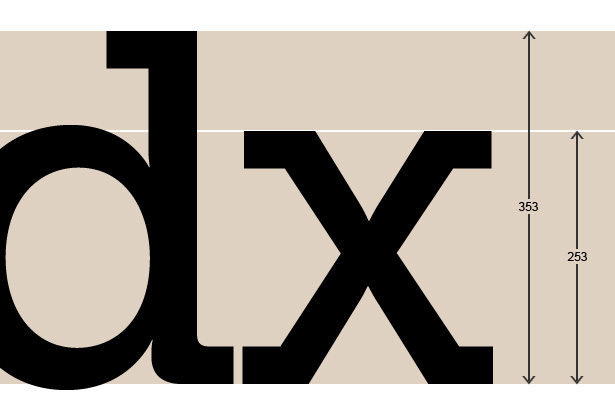
É claro que, se você tiver a sorte de ter acesso a um bom software de criação de fontes, poderá simplesmente abrir o arquivo de fontes que estará usando e ler a altura do x-height e do ascender.
Agora divida a altura x pela altura ascendente para encontrar a altura x como uma porcentagem do todo:
altura x altura / ascendente * 100 = segundo número de sementes
No caso da fonte no exemplo (que é Museo Slab), o resultado é:
253/353 = 0,71671388
ou 0.716em
Por que não estamos medindo do topo do ascendente até o fundo do descensor? Como os caracteres não tendem a ter um ascendente e um descendente (uma exceção ocasional sendo a letra 'f') e consequentemente os relacionamentos dentro das formas que compõem o design da fonte são baseados na relação entre a altura x e uma raiz mais longa. É possível medir o descensor, mas como a altura do boné (a altura dos capitéis) é geralmente muito próxima do ascendente, essa é a minha preferência. Se você se encontrar usando um tipo de letra com uma qualidade mais dominante - o contraste na espessura de traços diferentes, por exemplo - você pode querer usar esse valor no lugar da relação ascendente para x-altura.
A determinação de como chegar ao seu segundo número de sementes é uma das principais decisões de design que você terá que tomar, no entanto, não é algo para agonizar; escolha um número de um chapéu, se preferir, e siga em frente, as coisas boas ainda estão por vir.
Vale a pena notar que se você mudar a equação ao redor e dividir a altura ascendente pela altura x, você terminará com um número maior que um. Nesse caso, sua sequência será mais abrupta e um pouco mais dramática.
Criando nossa sequência
Então, nós temos nossos dois números de sementes: 1em e 0.716em e temos a fórmula n = n-1 + n-2:
1 + 0,716 = 1,716
0,716 + 1,716 = 2,432
1,716 + 2,432 = 4,148
etc.
Que resulta na seguinte sequência:
1, 0.716, 1.716, 2.432, 4.148, 6.58, 10.728, 17.308, 28.036… ad infinitum
O bit de design
Até agora, escolhemos nosso caminho através de algumas matemáticas básicas, mas úteis, e chegamos a uma sequência que nos dá uma variedade de tamanhos de 1em a 28.036em e além, se necessário.
Agora podemos usar esses valores como nossos tamanhos de tipo sequencialmente para criar um esquema de tipos bem proporcionado:

Você notará que começamos com p definido como 0.716 e h4 definido como 1, apesar do fato de que isso não é sequencialmente correto. A razão é que, em termos de hierarquia, h4 é mais importante que p. Nossa Seqüência de Lucas não deve ditar a hierarquia na página, dita as relações de escala de diferentes elementos. Apenas o seu conteúdo pode ditar a hierarquia .
Como não estamos restritos a valores consecutivos em nossa sequência e somos capazes de escolher quais números inteiros usamos, sempre alcançamos ritmo e estrutura com a mesma sequência. Mesmo se tomarmos uma abordagem muito dramática:

Exatamente a mesma sequência de Lucas também pode ser usada para criar um esquema mais reservado e semelhante a negócios:

A essência deste sistema é que as relações de escala são mantidas, a hierarquia é proporcional, mas há uma enorme variedade disponível para o designer. É aqui que você deve ganhar seu dinheiro: selecionando os tamanhos na escala para criar hierarquia e ênfase.
Flexibilidade
Frequentemente, o tamanho do tipo é ditado mais do que a ênfase: problemas de acessibilidade surgem quando estamos falando de um público com dificuldades visuais; o grande volume de conteúdo pode criar restrições; talvez precisemos ser flexíveis - literalmente - ao projetar um layout fluido.
Felizmente, o CSS lida com essa situação com facilidade. Como estamos usando o ems para nossos tamanhos, podemos configurar nosso tipo usando nossa Seqüência de Lucas e dimensionar o todo, definindo um tamanho padrão na tag body, mantendo o ritmo de nosso design, mas aumentando ou diminuindo os valores reais.

Observe nesta imagem que os tamanhos p, h2 e h1 permanecem os mesmos, todos retirados da nossa sequência. É a variação no tamanho da fonte da tag body (0.8em à esquerda e 1.4em à direita) que desce em cascata, criando resultados radicalmente diferentes.
Finalmente
Como dependente da matemática subjacente como este sistema é, é importante reconhecer que o design não pode ser reduzido a um conjunto de equações. Esse método de dimensionamento lhe dá uma estrutura com a qual trabalhar e o ajudará a criar esquemas de tipos bem proporcionados, mas cabe a você como designer usar o sistema como uma ferramenta, não como uma muleta.
As notas e escalas na música, até mesmo no Jazz, podem ser reduzidas a um conjunto de equações que descrevem seu relacionamento, mas é preciso alguém como John Coltrane para dar vida a esses relacionamentos.